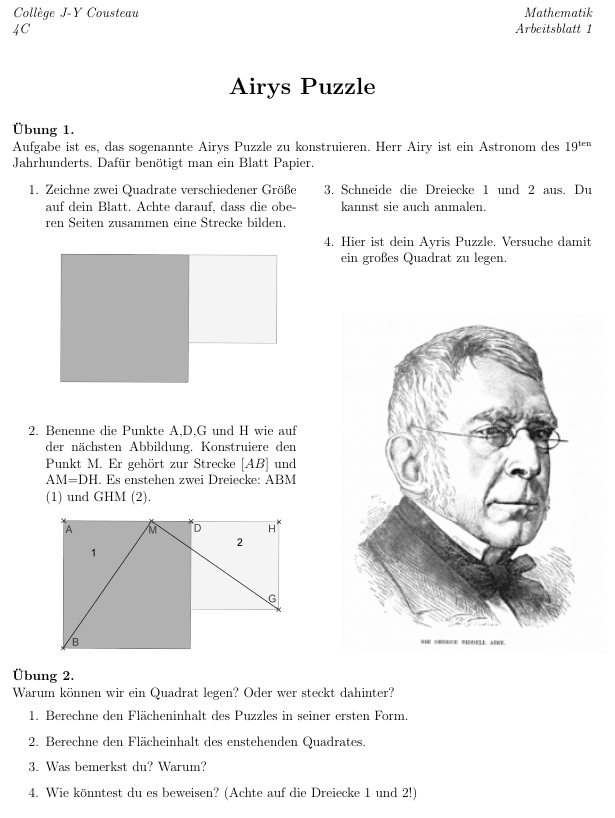
Dans cet article, je vous présente mon expérimentation des problèmes DUDU des frères Durand. Vous trouverez toutes les références de ces travaux sous licence CC en fin d’article.
Comme Arnaud Durand est très partageur et a de très bonnes idées, il tient un site Mathix.org, sur lequel il présente une grande partie de son travail. Ces travaux sont rarement réalisés seuls et au-delà du partage, on sent une très forte volonté de travailler en équipe. J’avais donc remarqué l’apparition de ses problèmes DUDU grâce à son compte Twitter @durandarno. Nous en avions discuté avec Stéphanie de Vanssay (alias @2vanssay sur Twitter) lors de notre rencontre en juillet 2013.
Un détail avait quand même piqué ma curiosité : était-ce réellement des jumeaux ? Ou alors un excellent montage ? La réponse n’est pas bien difficile et se trouve dans le paragraphe précédent, je vous laisse chercher et répondre par vous-même.
Et puis, il faut avouer que je me suis rendu compte qu’il y a des profs qui osent des trucs incroyables. Pour moi qui suit jeune prof, cela donne envie de dépasser pleins de frontières et pour cela Twitter est un endroit magique.
J’ai donc décidé de tenter l’expérience de ces problèmes DUDU. Tout simplement avec le premier épisode, avec le soutien d’Arnaud qui a non seulement les compétences techniques pour la réalisation des films mais également de grandes qualités de formateur et de pédagogue pour tous les étages. En profiter (au bon sens du terme), c’était donc rendre honneur à son travail.
Mes élèves étaient en 4ème, dans une classe où j’étais professeur principal. Peu travailleurs, volontiers chahuteurs et d’un niveau assez faibles, ils étaient le public idéal pour essayer quelque chose de différent. Redonner de la motivation à l’enseignant et à la classe, assouvir la curiosité des deux parties avec un tel projet. Se lancer ainsi relevait pour moi d’une autoformation en étant accompagné.
J’avais envie de voir la curiosité dans le regard des élèves, envie de voir des élèves perdus s’insestir. J’avais envie de le faire pour moi, pour les élèves. Et cela était possible avec un accompagnement de qualité, le rêve.
Le contact a donc été pris avec Arnaud. D’abord par Twitter. Vous noterez que grâce à la licence sous laquelle il a placé ses travaux, il n’est même pas nécessaire de le contacter pour utiliser ses travaux ! Nous sommes ensuite rapidement passés au mail, permettant l’envoi de fiches et de discuter de façon plus approfondie. Enfin, grâce à Skype, à quelques jours de mon saut dans le grand bain, j’ai pu recevoir les derniers encouragements nécessaires à me rassurer. Cette discussion a été très enrichissante et a permis une ouverture vers d’autres possibles : l’évaluation par compétence, l’évaluation positive, le contrat de confiance à la Antibi.
Puis, je suis passé à la pratique après une préparation aussi minutieuse que possible (mais, là j’atteins rapidement mes limites!) Il y aurait trois séances à une semaine d’intervalle chacune. Cela tombait en plein milieu d’une inspection qui a vu d’un bon œil ce travail. La première séance était le jour d’une autre première, celles des #KopfRechnen (un billet à venir là-dessus).
Je suis arrivé tôt et j’ai placé les tables en îlot. J’ai préparé les trois ordinateurs permettant aux élèves de consulter librement des ressources de leur choix. La vidéo tournait déjà sur le VPI lorsque les élèves sont entrés dans la salle :
J’avais amené pleins de pièces de 1ct et des échiquiers (j’y reviendrai). Les élèves devaient donc sur les trois semaines, rechercher une solution au(x) problème(s) posé(s) par la saynette et présenter lors de la dernière séance leurs résultats à la classe à l’aide d’un poster affiché ensuite. En classe, j’ai autorisé l’utilisation des smartphones. Les élèves avaient accès aux ordinateurs. A la maison, ils pouvaient procéder comme ils le souhaitaient.
Voici leurs productions :
Selon le souhait d’Arnaud, j’ai pris soin de masquer certains éléments de réponse.
Maintenant que le travail est terminé et que j’ai un peu de recul, je peux tirer un certain nombre d’enseignements de cette expérimentation. A chaud, j’étais fortement déçu mais en re-regardant les productions en fin d’année, je me suis dis que l’objectif principal était atteint : les élèves avaient fait des mathématiques autrement. Ils avaient réfléchi et produit des choses même si celles-ci n’étaient pas forcément celles que j’attendais.
Les élèves ont eu d’excellentes notes pour ce travail et ils en étaient ravis. Ils étaient tous en réussite car ils ont produit. Ils ont fait des maths, comme un mathématicien fait des maths : ils ont cherché avec tous les moyens possibles, ils ont échangé, ils ont parfois trouvé et ils ont toujours exposé leurs travaux. Par contre cela a mis en évidence la difficulté du travail en équipe, en particulier lorsqu’il s’agit d’un travail peu guidé sur le long terme.
Pour ma part, j’ai tout d’abord l’immense satisfaction d’avoir essayé ! Cette expérience a été très enrichissante car j’ai tenté des choses différentes que je n’aurais jamais osées seul, de la même façon que mon premier travail avec la video (Qui veut gagner des millions) avait été impulsé par une formation. La prochaine fois, car je recommencerai, je ne donnerai pas dans ce cas précis d’échiquiers et de pièces. Cela a trop orienté les élèves vers une méthode de comptage. Cela a bridé l’imagination des élèves. Je supprimerai également les propositions de sous-questions que j’avais proposées (du style, quelles sont les questions posées ? , quelles sont les données de l’énoncé ?) car les élèves trop scolaires ont cru que c’était uniquement à cela qu’il fallait répondre.
Je recommencerai car il est fondamental pour les élèves d’apprendre à travailler à plusieurs et d’être acteurs de leur apprentissage.
Je recommencerai car il a été super de travailler avec un autre collègue d’un autre coin de la France.
Je recommencerai car les élèves doivent être formés à avoir un regard critique sur ce qu’ils voient à la télé.
Je recommencerai car une telle activité permet entre autre d’éduquer au numérique.
Merci à la 4D !
Merci aux Dudu !
Les élèves au travail :
Voici les liens :
Les problèmes DUDU (deux saisons à ce jour)
Mathaloué
Le site d’Arnaud avec plein d’autres bonnes idées
Les résultats des TraAM sur les problèmes ouverts avec les TICE.